• 数学上一种求两正整数最大公约数的方法。

辗转相除法(Algorithm of division)

历史演进

在解决数学的难题上，为了因应复杂且时常遇到之问题，数学家研发出许多固定之算法或者公式，来帮助人民计算，而

此将先行介绍三大事件的时间发生。首先为欧基里德运用机械性的方式来求出最大公因数，而其机械式实质为一种偷工减

料的计算手段，利用一些制式化的步骤，而省略较繁复的手续，进而结合成机械化的模式，第二为艾尔法利兹米于应用问

题上的贡献，他发明出现今看似平常的移项法，来帮助人们解决问题，最后则是进入电脑的计算上。而在此历史演进中，

以下将特别介绍欧基里德的机械式方法，此即为辗转相除法。

计算步骤

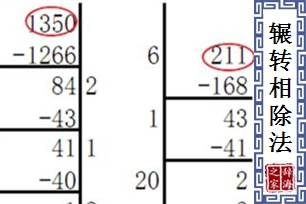
辗转相除法中，主要针对两者很大的数，其不易利用短除法来求初其公因数，因其研发出辗转相除法之方式。首先将两

者数字放于左右两边，并且于最左边、两数字之间以及最右边，分别画上三条直线，以做区隔，接着将较小的数于较大的

数底下在书写一遍，并且相减的动作，因此其所得之结果，再与原本未经处理的较小的数做比较，求其最接近之倍数后，

则再乘上此倍数后一样书写于下方，并做相减的动作，接着则将其结果再与第一次相减之结果做比较，如此周而复始的操

作，直至有一边相减后数字为0时，则可停止此操作，而可得到最大公因数即为另一边的最后数字。透过上述讲解，可了

解到辗转相除法，即为于左右两边做相乘相减的动作，因此才有辗转之名称由来。(注1)

举例

举一例子做实际演练，如391与493，将此放于左右两边且画上分隔线后，则开始进行操作，首先将391写于493的下

方，相减后得到102的结果，此时将102与未经处理之391做比较，可知倍数为3时最接近且不超过，因此将

102X3=306写于391下方，相减后得到85之结果，同样85与102最接近为1倍之关系，因此直接将85书写于102下

方，相减后得到17，此时再将17与85做比较，可知恰为5倍关系，而则将17X5=85书写于85下方，因此相减后结果为

0，此时即可停止运算，得到最大公因数即为0旁边之数字17。(注1)

关键字

中文关键字：辗转相除法

英文关键字：Algorithm of division

参考资料

注1 仲田纪夫/着。小学生数学大疑问，2001年初版，页124~125。国际村文库书店有限公司。

注2李嘉淦/着。中学数学科教材教法，1986年初版，页232~233。千华出版公司。